卢卡斯数列股票怎么运用?
卢卡斯数列股票怎么运用
接下来具体说说
从梅森数到卢卡斯数列(续)
(写在开头的废话)
还是有必要说一下:为啥正文只能发张图片?原因是,正文中大量使用了公式,而,
- 公式一多,头条的公式编辑器就会出错,无法使用;
- 图片只能表示行间公式,对于行内公式无能为力;
以上。
本续篇非常简单,几乎只用到了 初中数学知识,相信不会对各位造成数学上的压力,大家总算是可以以娱乐的心情看了。
每个做过核酸检测的人,都对于排队印象深刻,而志愿者更是如此!从“大白”的角度看,那长长的队伍长龙,见首不见尾。将排队中的人 替换 成数字,就成了 数列 ,替换成 函数,就是 函数列 。
除了等差数列外,最基本的数列是 等比数列,它的递推定义是:
- 初始条件:
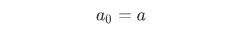
- 递推关系式:
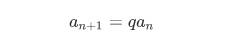
函数列的部分和组成的函数列,叫做 级数 ,最有名的 就是 幂级数:
- 幂函数列:
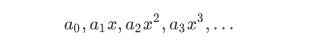
- 幂级数:
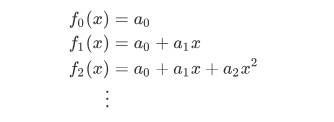
为了方便,记为:
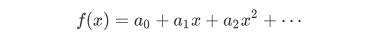
幂级数的系数 和 某数列 一一对应,因此 前者称为 后者的 母函数 ,使用 母函数 可从数列递推关系求出 通项公式,例如:上面的等比数列,令母函数为:
根据递推关系式,有,
再根据初始条件,求得母函数为 ①,
利用常用幂级数展开式,
将 qx 看成 x,则 g(x) 可展开为:
于是可得的 等比数列的 通项公式为:
看到这的各位 可能会直摇头,这不是简单的问题复杂化了吗?按照,递推定义 我直接就可以写出,等比数列的各项,这立即就能得出上式。
您先别急,如果所求是如下递推定义的通项呢?
- 初始条件:
- 递推定义:
您可以直接写出来,看看是否可以找到规律,反正 小石头是 不能。但是可以使用母函数,有,
于是求得母函数为:
接着,就是找它的展开式了,暴力的方法就是迈克劳林公式,但是这里有更巧妙的方法。
我们已经知道了 ①处母函数 对应的展开式系数是 等比数列,于是就可以考虑将上式的分数形式 列项为 两个 ①处形式 之和。
于是令,
为了将左边变成多项式因式分解的形式,可令 x = 1/y 带入,有,
化简得到,
这说明,α 和 β 是方程 ②:
的两个根,于是解方程得到,
再设,g(x)的列项为,
于是根据 ① 处的结论,得到 通项公式:
又因为,
比较等式两边分子多项式的各项系数,可列出如下线性方程组:
于是,解方程组求得 A 和 B 为,
而根据 韦达定理,由 方程 ② 知 p = α + β ,于是,最终得到:
令 p=P, q=-Q,考虑 a=2, b=P 的特殊情况 v n ,此时有,
于是 v n 的通项公式是:
再 考虑 a=0, b=1 的特殊情况 u n ,此时有,
于是 v n 的通项公式是:
其实,它们就是正文中我们将要讨论的 卢卡斯数列 。
从梅森数到卢卡斯数列
话题:#科学 ##科技# #数学# #算法#
小石头/编
(写在开头的废话)
素数公式素数一直是人类的梦想,可是这非常非常困难,一时半会儿怕不是也搞不出生产全部素数的公式,退而求其次,有两个方向:
- 找素数分布的统计规律;
- 找生成素数子列的公式;
这第二个方向就是我们今天要讨论的话题。历史上,有无数的数学家,在这个方向上探究过,其中比较有名的是:
- 梅森数 Mp=2ᵖ-1 (p 为素数);
- 瓦格斯塔夫数 Wp=(2ᵖ+1)/3 (p为奇素数);
- 费马数 Fn = 2²ˆⁿ + 1 (n为自然数);
虽然,这些公式都失败了(存在产生合数的情况),但是它们却发挥着意想不到的作用,而且他们还都有自己的推广形式。
其实还有很多整数,它们的产生与素数公式无关,其中著名的有:
- 完全数:真因子之和等于自己;
- 亲和数:一对真因子之和等于对方的数,例如:220与284(大家可以自己演算);
- 三角数:∑₀ⁿ (2k+1);
研究整数的学问就是数论,早期的数论就是算术,起源于 古希腊的 丢番图(著有 《算术》一书),后来一度沉寂,直到 文艺复兴时,欧拉和费马 两位大神 才开启了 数论的研究。而 高斯 和 勒让德 使得 《初等数论》发展到了一个新高度。
时代变迁,数学发生了,两次根本性变革,其一:微积分的诞生标志着 分析时代的到来,其二:群论的发现标志着 抽象代数王朝的降临。数论学家也以他们作为研究对象,变革着 数论的研究方法,至此 数论有了两条分支:《解析数论》和《代数数论》。
据说还有以几何为工具的《几何数论》,这个小石头 实在是 没有接触过,有哪位大神 可以给大家科普一下吗?
时至今日,素数公式,依然是民间讨论较多的数论问题之一(哥德巴赫猜想、孪生素数猜想 和 黎曼猜想 是另外的热门问题),我相信头条的数学爱好者中也一定有创造自己(不完全)素数公式的数的人。
如果你有兴趣,也可以不妨试一试。也欢迎大家在评论区讨论!
以上就是卢卡斯数列股票怎么运用?的详细内容,希望通过阅读小编的文章之后能够有所收获!
