知道两组的样本量均数加减标准差怎么比较？

知道两组的样本量均数加减标准差怎么比较

接下来具体说说

连续变量假设检验 之 两*样本t检验

统计概述

前面一节讲到的是单样本t检验是针对一个样本与已知总体样本均值之间的检验，但在实际工作中，我们会遇到 两个样本之间的均值检验 ，这个如何解决呢？我们有法宝，SPSS提供的两*样本t检验。

两*样本t检验的 目的 ：两个样本在 相互* 的前提下，检验两个样本的 总体均数 是否存在 显著性差异 。尤其当两组样本量相等时，两个样本均数之差的抽样误差最小，检验效能*高。需满足条件：

• *性： 各观察值之间是相互*的，不能相互影响
• 正态性： 各个样本均来自于正态分布的总体
• 方差齐性： 各个样本所在总体方差相等

在实际应用中，*性对结果影响较大，但检验数据*性的方法较复杂，一般都是根据资料的性质加以判断，如遗传性基本、传染病数据可能存在非*的问题。如果从专业背景上可以肯定数据不存在这些问题， 则一般*性总是能够满足的 。

由上描述可见，两*样本t检验所需的是两组样本，这两组样本获取有两种可能：

• 靠前：随机分组 ，如60只SD大鼠，随机分为2组，每组30只，分别接受不同的处理，然后比较不同指标差异
• 第二：按照某种属性特征进行分组 ，如班级可分为男性与女性，然后比较男女之间的成绩差异

SPSS实现

示例：采用完全随机设计的方法，将19只体重、出生日期等相仿的小白鼠随机分为两组，其中一组喂养高蛋白饲料，另一组喂养低蛋白饲料，然后观察喂养8周后各小白鼠所增体重（mg）情况，问两组膳食对小白鼠增加体重是否相同？

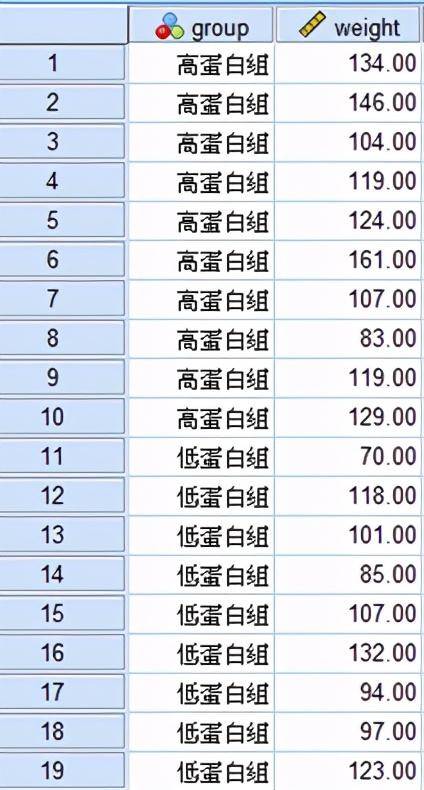
1. 建立假设：建立检验假设，确定检验水准 α

• H0： μ1= μ2 ，即高蛋白组与低蛋白组所增体重的总体均数相同
• H1： μ1 ≠ μ2 ，即高蛋白组与低蛋白组所增体重的总体均数不同
• α = 0.05，即置信区间为95%

2. 检验数据是否符合 正态分布

• 打开 分析—描述统计—探索
• 输出结果与说明

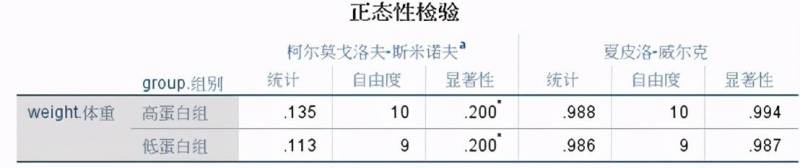
从上表可看出，高蛋白组和低蛋白组的 P均大于0.05 ，说明两组数据呈 正态分布 。

3. *样本t检验

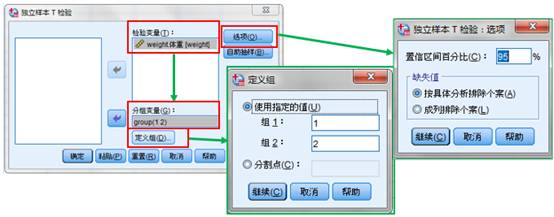
（1） 打开 分析—比较平均值—*样本t检验

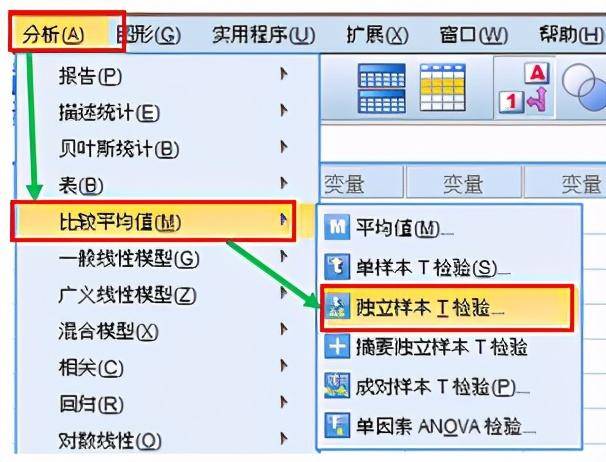
（2） 参数说明

• 检验变量： 进行t检验的目标变量，变量值为数值型
• 分组变量： 用于对检验变量进行分组，为分类变量
• 定义组---使用指定值 ：在组1、组2中输入分组变量值
• 定义组---分割点 ：通过分割点将分组变量分为两组，一组大于等于分割点数量，一组小于分割点数量
• 选项： 设定置信区间和缺失值处理方式

（3） 输出结果与说明

• 基本统计量： 在下表中列出了样本量、平均值、标准差和标准误。

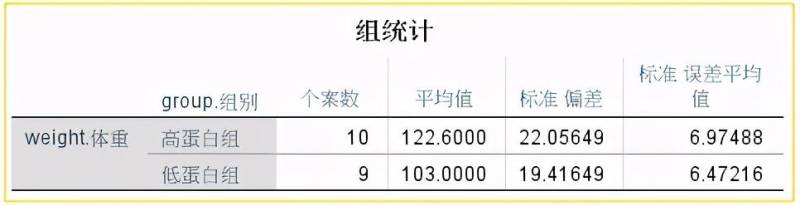
• 两*样本t检验

在*样本检验表格中，前两列是 Levenes方法 对两组数据进行 方差齐性检验的结果 ，可看出F=0.035， p=0.853>0.05，所以显示两组数据的方差齐 。

后面7列是对两组数据均数比较t检验的结果，分为两行，靠前行对应的是方差齐的结果，下面一行对应的是方差不齐的结果。

本次数据是方差齐，所以查看靠前行结果，t=2.045，df=17， 显著性p=0.057>0.05，所以可认为高蛋白组和低蛋白组小白鼠之间体重增加量的差别无统计意义 。

高蛋白组和低蛋白组的平均值差值为19.6，标准为9.58；两总体均数差值的95%置信区间[-0.61748, 39.81748]。在默认状态下，SPSS计算的是95%置信区间。

4. 语法

比起两组均数比较分析，这两种分析更值得你注意

最近小编发现头条上的用户们对SPSS数据分析还是比较了解的，基础比较好呢，看来我的文章太基础了，很少人阅读，不过我更新文章从易到难，陆续看下来，后面应该更轻松掌握，希望多多支持！我后期去找些更有意义的分析知识来分享。下面我们进入正题：

---

在上一期，我们介绍到了两样本均值的比较，但是现实中很多情况下，需要比较两组以上的均值，本章介绍的就是专门解决这一问题的。

1、 单因素方差分析

单因素方差分析是研究同一个因素的不同水平，均值是不是存在统计意义；与之相对应的多因素分析，则是研究多个因素的均值，我们下期会分享相关知识。

方差分析的 应用条件 ：

（1） 总体服从正态分布；

（2） 总体具有方差齐性；（P>0.05，则认为方差相等，具有方差齐性）

（3） 两观察值之间没有系统相关性；

此次研究的是不同学历的人焦虑情况是不是存在差异。

SPSS操作如下：分析——比较均值——单因素ANOVA检验——勾选描述、方差齐性

方差分析主要是看ANOVA表（在此之前也需要看是否存在方差齐性）

2、 非参数检验——Kruskal-Wallis法

当数据无法用方差分析来解释数据时，就需要运用Kruskal-Wallis法，一般最常用的也是K-W法，也称H检验；

SPSS操作如下：分析——非参数检验——K个*样本——

结果输出：

解释类似*样本检验，主要是看显著性。

以上就是知道两组的样本量均数加减标准差怎么比较？的详细内容，希望通过阅读小编的文章之后能够有所收获！