如何用correl求股票的相关系数?
如何用correl求股票的相关系数
十九、计算平均绝对离差(AVEDEV函数):各变量与总体平均值之差叫离差,离差的绝对值的平均值就是平均绝对离差。其计算公式如下:其中:为参数变量,为参数均值,为参数个数。接下来具体说说
如何用correl函数挑选合适的基金组合?
我们知道,一只公募基金一般一个个股最大的仓位不超过10%,这主要是为了防范个股的黑天鹅风险,但一只基金毕竟只能代表一种风格,比如说沪深300只代表了A股规模前300只股票,为了享受各种风格的上涨,进一步降低风险,很多人做了基金组合。那么问题来了,什么样的基金适合做组合呢?
我们先从2个基金说起,就像中药里的配伍一样,什么样的基金不适合组合?什么样的基金适合组合?这里我们要引入一个重要的参数,叫相关系数,这个参数的计算有点复杂,这里不详细介绍了,我们还是以实用为主,好在excel里有个correl函数可以直接算出相关系数,
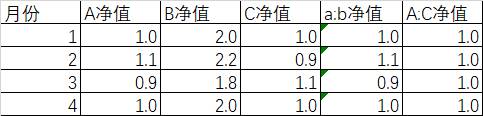
我们先举个简单的例子来说明问题,我们假定有3个基金分别为A、B、C三只基金,4个月的净值变化如图,我们从4个月的净值变化可以知道,B基金只是A基金的净值放大了1倍,而C基金的涨跌正好和A、B相反。如果我们计算A和B的相关系数,那么可以用correl(b2:b5,c2:c5)=100%,也就是说A、B两只基金的净值虽然数值不同,但它们是100%相关的,如果我们计算A和C的相关系数,我们可以用correl(b2:b5,d2:d5)=-100%。也就是完全不相关。
相关系数小有什么好处呢?我们看到如果同时平均持有A和B两只基金,那么到了第二个月组合的净值还是涨到了1.1,第三个月组合的净值还是跌到了0.9,根本没有起到分散风险的作用,而A和C的组合,因为是负相关,所以第二个月、第三个月的净值还是稳定在1。当然为了说明问题,这里举的例子是一个极端简单的例子,实际上没那么简单。我们举个实际的例子。
我们选了三个对应指数份额最大的指数基金:跟踪沪深300的华泰柏瑞沪深300指数基金、跟踪上证50的华夏上证50指数基金、跟踪标普500的博时标普500指数基金,从2013年12月6日到2020年1月16日,华泰柏瑞300和华夏50用correl计算出来的结果,相关系数高达95.96%,而华泰柏瑞300和博时标普500的相关系数才49.08%,显然如果你买了华泰柏瑞300在配置华夏50的效果就不如配置博时标普500了,从持仓分析,其实也是这样,上证50的50个个股,其实都已经包含在沪深300的300个个股里面的,所以试图通过组合达到分散风险是很难的,相反如果配置了标普500,那么就起到了分散风险的目的。
这里有几个问题要注意,靠前基金的净值要进行等比复权,所谓等比复权,就是分红后马上再投入到这个基金中去,不过我们最常用的通达信的默认值不是等比复权的,这个开关比较深,在“系统设置”-“设置1”的“复权使用等比方式”里,默认是不打勾的,只要打钩了就可以了。第二我们说的低相关品种的选择,有一个最重要的前提,就是这些品种都是长期往上的,如果配置了虽然相关系数小甚至负相关但长期是往下的,虽然可能波动小了,但收益率受到非常大的影响,这也不是我们做基金组合的初衷。也就是说,相关系数小只是基金组合的必要条件,而不是充分条件。
excel函数公式大全之利用CORREL函数FORECAST函数预测未来销售额
excel函数公式大全之利用CORREL函数与FORECAST函数的组合预测未来冷饮销售额。xcel函数与公式在工作中使用非常的频繁,会不会使用公式直接决定了我们的工作效率,今天我们来学习一下提高我们工作效率的函数CORREL函数FORECAST函数。在日常工作中我们会发现有些数据之间存在着一定的联系,比如温度与冷饮的销量,因此我们可以根据已经统计的温度与销量对应的数据来预测冷饮未来的销量。具体的例子如下图所示:
首先根据已有的温度与销售额的数据,计算温度与销量之间的相关系数,利用CORREL函数就可以计算出温度与销售额之间的联系。
我们首先来认识一下CORREL函数,公式-----**函数----输入CORREL-----单击确定
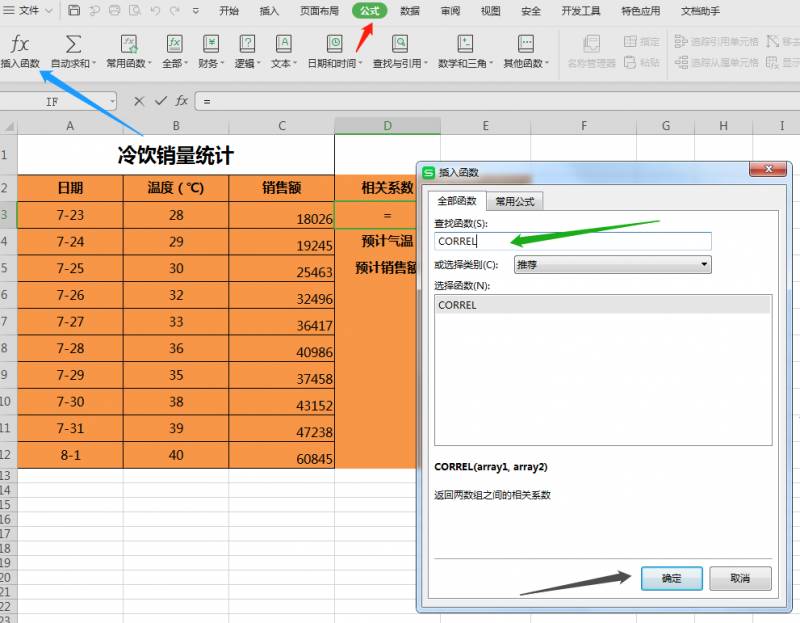
CORREL函数有两个参数构成,靠前个参数靠前组数值,第二个参数第二组数值。根据一二组数值,CORREL函数会自动计算出二者之间的相关系数。
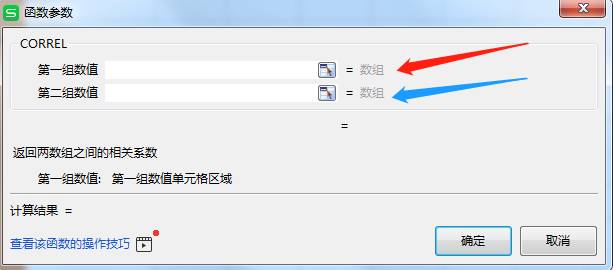
我们利用CORREL函数计算温度与销售额之间的相关系数公式为:=CORREL(B3:B12,C3:C12)
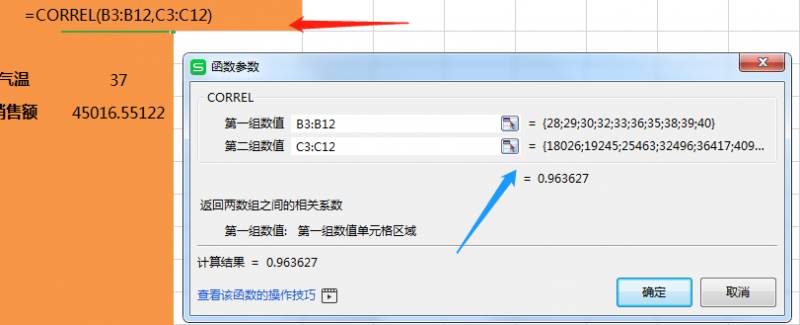
我们利用CORREL函数计算出温度与销售额之间的相关系数为0.96362,这说明温度与销量呈正相关,且具有很高的相关性。
根据CORREL函数计算出的相关系数,在利用FORECAST函数预测某一温度时的销售额。
我们下面来认识一下FORECAST函数,公式-----**函数----输入FORECAST-----单击确定
我们会发现FORECAST函数有三个参数构成,预测点X值也就是我们要预测的温度。第二个参数已知Y值合集也就是我们已经统计的销售额,已知X值合集也就是我们已经统计的温度。
利用FORECAST函数预测某一温度销售额的具体公式为:=FORECAST(E4,C3:C12,B3:B12)
我们一起来回顾一下要根据已经统计的数据预测未来某一数据下的销售额时,靠前步要利用CORREL函数判断两组数据之间是否存在相关性。如果两组数据之间存在相关性,我们在利用FORECAST函数,根据要预测的数据自动生成我们要预测的销售额。
谢谢大家的观看,我们下一期再见,如果有什么问题欢迎评论区留言或私信我们,如果有你想知道的函数公式,可以告诉我们,我们及时为你解答。
自学Excel之35:统计函数(四)
十九、 计算平均绝对离差( AVEDEV函数 ) :
各变量与总体平均值之差叫离差,离差的绝对值的平均值就是平均绝对离差。其计算公式如下:
其中: 为参数变量, 为参数均值 , 为参数个数。
语法是: “=AVEDEV(number1, [number2], ...)” 。
参数:number1, number2, ... number1是要计算离差的一组数字或者包含数字的名称、数组或引用的参数。
例: 计算表中参数的平均绝对离差。
在C2单元格**函数: “=AVEDEV(A2:B6)” ,按【Enter】键确认。
计算平均绝对离差
二十、 计算离差的平方和( DEVSQ函数 ):
DEVSQ函数用于计算各变量与总体平均值之差(离差)的平方和。其计算公式如下:
其中: 为参数变量, 为参数均值。
语法是: “= DEVSQ(number1, [number2], ...) ” 。
参数 number1, [number2], ...是用于计算离差平方和的 1 到 255 个参数。 如果参数包含文本、逻辑值或空白单元格,则将被忽略;但包含零值的单元格将计算在内。
例: 计算表中参数的离差的平方和。
在C2单元格**函数: “= DEVSQ (A2:B7)” ,按【Enter】键确认。
计算离差的平方和
二十一、 计算总体方差:
方差是每个样本值与全体样本值的平均数之差的平方和的 平均数 。
方差是与中心偏离的程度,用来衡量一批数据的波动大小。 在 样本容量 相同的情况下,方差越大,说明数据的波动越大、越不稳定。
总体方差是将整个总体当作参数来计算方差。其公式如下:
其中: 为总体方差, 为变量, 为总体均值, 为总体例数。
1、VAR.P函数:
VAR.P函数用于计算 基于整个总体的方差(忽略逻辑值和文本)。
语法是: “= VAR.P(number1,[number2],...) ” 。
参数 number1,number2,...是对应于总体的数值参数。
2、 VARPA 函数:
VARPA 函数 用于计算 基于整个总体的方差(包括逻辑值和文本)。TRUE 看作 1, 文本或 FALSE看作 0。
语法是: “= VARPA(value1, [value2], .. . ) ” 。
参数 value1, [value2], ...是对应于总体的所有参数。
例: 已知某物品的总体样本参数,分别用VAR.P函数和 VARPA函数 计算其总体方差。
1)在C2单元格**函数: “=VAR.P(A2:B7)” ,按【Enter】键确认;
2)在C4单元格**函数: “=VARPA(A2:B7)” ,按【Enter】键确认。
计算总体方差
二十二、计算样本方差:
在实际工作中,总体均数通常难以得到,一般应用样本代替总体参数来计算方差,即样本方差。其计算公式如下:
其中: 为样本方差, 为变量, 为样本均值, 为样本例数。
1、 VAR.S函数:
VAR.S函数 用于计算 给定样本的方差(忽略逻辑值和文本)。
语法是: “= VAR.S(number1,[number2],...) ” 。
参数 number1,number2,...是对应于样本的数值参数。
2、 VARA 函数:
VARPA 函数 用于计算 给定样本的方差(包括逻辑值和文本)。TRUE 看作 1, 文本或 FALSE看作 0。
语法是: “= VARA(value1, [value2], ...) ” 。
参数 value1, [value2], ...是对应于样本的所有参数。
例: 将上例中的已知参数看作是一个给定样本而不是总体,分别用VAR.S函数和 VARA函数 计算其样本方差。
1)在C6单元格**函数: “=VAR.S(A2:B7)” ,按【Enter】键确认;
2)在C8单元格**函数: “=VARA(A2:B7)” ,按【Enter】键确认。
计算样本方差
二十三、 计算总体标准偏差:
标准偏差是方差的算术平方根。
标准偏差也是用来测算与中心偏离程度的,但其计算单位和变量的相同,比方差清楚,因此分析的时候更多使用的是标准偏差。
总体标准偏差是将整个总体当作参数来计算 标准偏差 。其公式如下:
其中: 为总体标准偏差, 为变量, 为总体均值, 为总体例数。
1、 STDEV.P 函数:
STDEV.P 函数用于计算 基于整个总体的 标准偏差 (忽略逻辑值和文本)。
语法是: “= STDEV.P(number1,[number2],...) ” 。
参数 number1,number2,...是对应于总体的数值参数。
2、 STDEVPA函数:
STDEVPA函数 用于计算 基于整个总体的 标准偏差 (包括逻辑值和文本)。TRUE 看作 1, 文本或 FALSE看作 0。
语法是: “= STDEVPA(value1, [value2], ...) ” 。
参数 value1, [value2], ...是对应于总体的所有参数。
例: 已知某物品的总体样本参数,分别用 STDEV.P 函数和 STDEVPA函数 计算其总体 标准偏差 。
1)在C2单元格**函数: “= STDEV.P (A2:B7)” ,按【Enter】键确认;
2)在C4单元格**函数: “= STDEVPA (A2:B7)” ,按【Enter】键确认。
计算总体标准偏差
二十四、计算样本标准偏差:
样本 标准偏差是将给定样本当作参数来计算 标准偏差 。其公式如下:
其中: 为样本标准偏差, 为变量, 为样本均值, 为样本例数。
1、 STDEV.S 函数:
STDEV.S 函数用于计算 给定样本的 标准偏差 (忽略逻辑值和文本)。
语法是: “= STDEV.S(number1,[number2],...) ” 。
参数 number1,number2,...是对应于样本的数值参数。
2、 STDEVA函数:
STDEVA函数 用于计算 给定样本的 标准偏差 (包括逻辑值和文本)。TRUE 看作 1, 文本或 FALSE看作 0。
语法是: “= STDEVA(value1, [value2], ...) ” 。
参数 value1, [value2], ...是对应于样本的所有参数。
例: 将上例中的已知参数看作是一个给定样本而不是总体,分别用 STDEV.S 函数和 STDEVA函数 计算其样本 标准偏差 。
1)在C6单元格**函数: “= STDEV.S( A2:B7)” ,按【Enter】键确认;
2)在C8单元格**函数: “= STDEVA (A2:B7)” ,按【Enter】键确认。
计算样本标准偏差
二十五、计算协方差:
协方差是两组数据离差乘积的平均值,方差是协方差的特殊情况,即当两组数据相同时的协方差。
协方差用于衡量两个变量的总体误差。如果两个 变量 的变化趋势一致,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,那么两个变量之间的协方差就是负值。
1、COVARIANCE.P函数:
COVARIANCE.P函数用于计算两组数据的 总体协方差。其公式如下 :
语法是: “= COVARIANCE.P(array1,array2) ” 。
参数 array1,array2是要计算协方差的两组元素个数相同参数。
2、COVARIANCE.S 函数:
COVARIANCE.S函数用于计算两组数据的 样本协方差。其公式如下 :
语法是: “= COVARIANCE.S(array1,array2) ” 。
参数 array1,array2是要计算协方差的两组元素个数相同参数。
例: 计算表中两组参数的总体协方差和样本协方差。
1)在C2单元格**函数: “=COVARIANCE.P(A2:A6,B2:B6)” ,按【Enter】键确认;
2)在C4单元格**函数: “=COVARIANCE.S(A2:A6,B2:B6)” ,按【Enter】键确认。
计算协方差
二十六、计算两组数据之间的相关系数(CORREL函数):
CORREL函数用于计算两组数据的相关系数。
使用相关系数可以确定两个属性之间的关系。 相关系数表示数组之间的正 (+1) 或负 (-1) 相关性。 接近 0 的相关系数表示无相关性或弱相关性。 其计算公式如下:
语法是: “=CORREL(array1, array2)” 。
参数:array1,array2是要计算相关系数的两组数据。
例: 计算成绩表中总成绩与上课天数之间的相关系数。
在G2单元格**函数: “=CORREL(E2:E8,F2:F8)” ,按【Enter】键确认。
以上就是如何用correl求股票的相关系数?的详细内容,希望通过阅读小编的文章之后能够有所收获!
