股票里的gamma是什么？

股票里的gamma是什么

期权作为一种金融衍生投资工具，相对于股票交易的逻辑主要是其价格的上涨和下跌, 期权具有独特的风险收益关系，需要投资者在交易的时候同时关注期权价格与时间流逝、标的资产价格、标的资产价......接下来具体说说

通俗易懂的介绍期权希腊字母（2）：Gamma

-- 这是忠伟的第 133 篇原创 --

学习期权的时候，大家经常会看到Delta、Gamma、Vega、Theta、Rho 等希腊字母。

一些朋友对于这些希腊字母觉得有些困惑。

为什么期权要引入这么多复杂的希腊字母？

主要是因为期权太灵活，它的价格变化是非线性的。

期权价格变化是由多个变量联合作用发的。

这些期权希腊字母，就是引起期权价格变化的重要量化指标。

学好“希腊字母”，能够让我们更为直观、全面、科学的评估我们仓位的风险暴露。

有助于我们更加合理、安全的管理我们的投资。

昨天我写了一篇文章，《通俗易懂的介绍一下期权希腊字母Delta》

今天准备给大家通俗易懂的介绍第二个希腊字母Gamma。

# 01 什么是Gamma

Gamma是Delta的导数。代表Delta对标的价格变化的敏感度。以股票期权来举例，就是表明当股票价格变动一个单位，Delta会变动多少个单位。

有些书也把Gamma说成是期权价格随标的价格变动的加速度。

这里举个例子，通俗易懂的给大家描述一下Gamma。

假设有一个股票 品夕夕的一个看涨期权，现在的Delta是0.6 （简单理解股票每上涨1元，期权价格上涨 0.6元）

我们知道，Delta值不是固定的，如果股价上涨，Delta值也会上涨。那么上涨多少呢？就是由Gamma值来决定的。

它的Gamma值是 0.05.

那么意味着，如果品夕夕的股价上涨1元钱，Delta会增加 1 x 0.05 = 0.05

那么新的Delta值就变成 0.6 + 0.05 = 0.65

通过这个例子，我们可以清晰的看出，Gamma值决定了期权Delta值的变化程度。

# 02 Gamma有什么特性

（1）Gamma值和期权的价格位置有关

当期权价格是深度实值的时候，此时期权几乎可以近似等同于股票。Delta的绝对值很大。Gamma值却很小。

此时股价变动，Delta值的变化也就很小。

当期权价格是深度虚值的时候，此时期权几乎可以近似等同于废纸。Delta的绝对值很小。Gamma值仍然很小。

此时股价变动，对Delta的影响也很小。

只有期权价格是平价期权的时候，此时Gamma最大，股价变动引起的Delta值变动会最大。

上面介绍的特性，可以在下图中形象的看出。

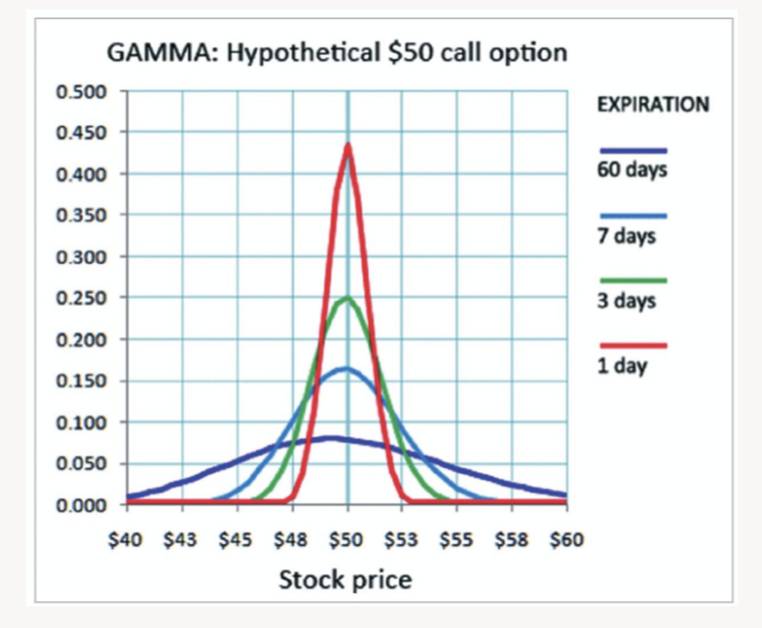
从上图可以看出，*高的Gamma值，发生在平价期权时。

（2）Gamma值和期权到期时间有关

Gamma值和期权到期时间的关系，非常复杂。

教科书上要讲很多篇幅。

这里，我们通过例子来说明。

有一个虚值看涨期权。

距离到期日很远的时候，此时Gamma值很小。

随着到期日的临近，此时Gamma值会逐渐升高。

但是当到期日非常临近了，此时Gamma值又会迅速下降。

这是虚值看涨期权的情况。

实值看涨期权的情形和虚值看涨期权类似。

对于平价期权，如果是到期日非常临近了，Gamma值不会下降，会继续升高。

下图可以形象的看出Gamma值随时间的变化。

红色曲线代表平价期权的Gamma变化

绿色曲线代表实值期权的Gamma变化

蓝色曲线代表虚值期权的Gamma变化

横坐标代表时间，最右侧是到期日。距离右侧越远，代表到期时间越长。

纵坐标代表Gamm值，也向上，代表Gamma越大。

# 03 投资中如何使用Gamma

Gamma值对于我们分析风险暴露，控制持仓风险，有很重要的作用。

（1）Gamma可以用来分析赚钱的速度

如果Gamma很大，那么意味着股价上涨或下跌的时候，你赚钱或赔钱的速度会很快。

如果Gamma很小，那么意味着股价变动的时候，你赚钱或者赔钱的速度会很慢。

比如距离到期时间很远的一个虚值看涨期权，它的Gamma值很小，股价上涨的时候，Delta值变化也会很小。那么赚钱的速度不够快。

但是随着到期时间的逐渐接近，Gamma值开始升高，此时股价上涨的时候，Delta值会变大，此时赚钱的速度会加快。

随着到期时间更加接近，临近到期日了。此时Gamma值又会下降，此时股价上涨，Delta值又会变小，赚钱的速度又会变慢。

这也是为什么我们选择期权的到期时间很关键。

过远或过近的到期时间，受Gamma值的影响，都会影响我们赚钱的速度。

但是此时要清楚一件事情。Gamma是一把双刃剑。赚钱的速度快了，赔钱的速度也会加快。

有时选择一个安全的策略，Gamma小一下，也不一定是坏事。

（2）Gamma值可以帮助我们控制风险

期权非常灵活

一个相同的仓位，在不同的时间点，或者不同的标的股价位置，风险也不同。

通过Gamma值，可以帮助我们分析当前持仓的风险是否比较高，帮助我们控制风险。

如果Gamma值过高，那么意味着我们的风险比较大。

比如一个持仓组合，在距离到期日有一段时间的时候，Gamma值不大，那么我们的风险是可控的。

但是随着到期日的接近。Gamma值可能迅速升高。

意味着我们的这个持仓，此时风险比较高了。

这时如果不想冒险的话，平仓是一个适合的选择。

# 04 总结

今天这篇文章，给大家通俗易懂的介绍了Gamma。

受篇幅所限，只能算是通俗易懂的入门。

让大家对Gamma这个概念，以及如何使用，有一个感性的认识。

更多细节，有很多的教科书都做了详细的介绍。

想深入学习的朋友，可以看一下之前推荐的《麦克米伦谈期权》。

这本书是麦克米伦写的，里面对期权的希腊字母，有更详细的介绍。

今天的文章就到这里，希望能给喜欢投资的朋友带来帮助。

-------

如何计算期权的Gamma值以及影响Gamma值的因素都有哪些？

假设一只股票的要素如下：

从Gamma值的计算公式可以看到，想得到Gamma的值靠前步是计算d1

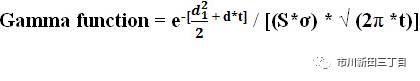
d1的的计算公式如下，结果等于0.2235

如果行权价，无风险利率，波动率和股息率等其他条件都不变，在股价为价外期权、价内期权与平价期权，中短长期限看涨期权所对应的伽玛值分别为：

可见，期权的期限和行权价格对伽马值均会产生影响。不管什么期限，在各个行权价对应的伽马值中平价期权的伽马值通常都是*高的；如果行权价相同，越短期限的伽马值越高，也就是期权的德尔塔值对资产价格的变动更 敏感 ，短期限的伽马值曲线会呈现比较完美的钟形曲线，价外期权和价内期权的伽马值会明显低于平价期权的伽马值。

浅蓝线为期权期限为3个月的伽马值曲线，橙线为期权期限为6个月的伽马值曲线，灰线为期权期限为12个月的伽马值曲线。

从0.25年的德尔塔值和伽马值的走势对比可见，随着股价上涨，价外期权先是变成平价期权，然后变成价内期权，看涨期权的德尔塔值随着股价的上涨逐渐增加，但在股价升过平价水平进入深度价内区间后，德尔塔值增加的速度明显放缓。

为什么会这样？原因在于期权的德尔塔值本质上体现的是期权在到期时变成价内期权的概率，而伽马值衡量的是这种概率变化的速度，当一个期权进入深度价内区间后，其德尔塔值将高度接近1，也就是当股价上涨1元，会导致期权价格也随之上涨1元，因此该看涨期权在到期日前不再成为价内期权的概率变得很渺茫，因此变化的速度出现明显下降。

还是以0.25年为例，波动率和伽马值的对应关系如下，可见波动率越高，价外期权和价内期权的伽马值与平价期权的伽马值之间的差距越小，伽马曲线就越平坦；波动率越低，价外期权和价内期权的伽马值与平价期权的伽马值之间的差距越大，伽马曲线就越陡峭，以下为波动率不同情况下的伽马值表现。

小结：

• 期权的行权价、存续期限和波动率等因素均会对伽马值的大小产生比较大的影响，无风险利率和股息等因素的影响力度相对较小；

• 伽马值的变化并非线性；

• 伽马值越大，期权费对资产价格的变动 敏感 性越高；伽马值越小，期权费对资产价格的变动 敏感 性越低；

• 期权的存续期限越短，伽马值就越大；期权的存续期限越长，伽马值就越小；

• 波动率越大，伽马值曲线越平坦，平价期权的伽马值就越小；波动率越小，伽马值曲线越陡峭，平价期权的伽马值就越大；

• 期权漫画系列七：期权希腊字母之Gamma和Vega

  期权作为一种金融衍生投资工具，相对于股票交易的逻辑主要是其价格的上涨和下跌, 期权具有独特的风险收益关系，需要投资者在交易的时候同时关注期权价格与时间流逝、标的资产价格、标的资产价格的波动率这三种因素，俗称时间、空间、波动率，之间的变化关系。刚开始接触期权的投资者可能会认为期权交易相对复杂而很难进一步去了解，但是在真正了解了希腊字母 – 期权价格变化的影响因素，相信大家会对期权头寸的精细化管理叹为观止，也为后面理解期权组合策略收益情况打好基础。

  昨天权漫画系列六 期权希腊字母之Delta，给大家初次讲解了靠前个期权希腊字母的含义，今天继续推出Gamma和Vega的详解。

  2、Gamma

  Gamma反映的是Delta对标的资产价格变动的敏感程度，即期权价格随着标的资产价格变化的加速度，因为如果Gamma较大，标的资产价格变动的时候会带动Delta的变化加快，进而导致期权价格的变化幅度增大。

  比如对于买入平值认购期权，Delta为0.5，若Gamma为0.1，那么标的资产价格上升1元，由于Gamma的影响，导致Delta增加0.1，变成0.6，说明期权价格对标的资产的变动更加敏感。如果单看策略中的Delta，标的资产价格变动幅度不足以完全覆盖期权价格的变动，所以Gamma是非常重要的希腊字母，衡量标的资产价格波动幅度对期权价格的影响，在期权交易中价格的波动不容忽视。

  Gamma的特点：

  1.对于认购和认沽期权的买方，标的资产上涨或者下跌会为投资者带来收益，所以对于任意行权价格，Gamma大于零。

  2.反之对于认购和认沽期权的卖方，对于任意行权价格，Gamma小于零。

  3.当行权价格等于标的资产价格，即对于平值的认购和认沽期权来说，标的资产价格的变动对期权的性质会产生较大的影响，波动性较强，所以平值期权的Gamma相对虚值和实值期权较大。

  Gamma的应用：

  Gamma衡量Delta中性策略对冲的误差/风险。

  比如对于上述买入平值认购期权的案例，若标的资产价格上升1元，为了保持Delta中性策略，就不仅仅只对冲原来0.5的Delta，还需要考虑Gamma对Delta带来的那0.1的增量。因此进行Delta中性对冲时，Gamma越大，Delta变化的就越快，对冲的风险和难度也越大，反之亦然。

  3、Vega

  Vega是衡量标的资产价格的波动率对期权价格的影响程度。即波动率上涨（下跌）1%，期权价格上涨（下跌）的变化量为Vega。无论对于认购还是认沽期权，只要是期权的买方，持有头寸的Vega大于零，希望波动率增大；期权的卖方，持有头寸的Vega小于零，希望波动率越小越好。

  Vega是考虑波动率的变化对期权价格的影响。可能买入一个隐含波动率为20%的标的资产，价格为100元，一周后标的资产的价格还是100元，但是隐含波动率下降到15%，那么对于期权的买方，即做多Vega的一方，是亏损的。

  Vega的特点：

  1.对于认购和认沽期权的买方，波动率上涨会带来收益，即Vega大于零。

  2.反之对于认购和认沽期权的卖方，波动率下跌会带来收益，所以Vega小于零

  3.和Gamma的特点相似，平值期权随着标的资产价格的变动，期权在到期是否会被行权的不确定性最大，即期权价格对标的资产价格的波动率最为敏感，所以平值期权Vega最大。

  Vega的应用：

  今天（11月27日）早市收盘时50ETF价格为2.993元/份，对应行权价格为3元的平值认购50ETF期权近月合约的价格为0.0028元/份，行权价格为3元的平值认沽50ETF期权近月合约的价格为0.009元/份，两者vega均为0.0006。在50ETF价格的波动率上升（下降）1%时，平值认购和认沽期权的价格均上涨（下跌）0.0006，即平值认购期权价格上涨至0.0034元/份，或下跌至0.0022元/份；平值认沽期权价格上涨至0.0096元/份，或下跌至0.0084元/份。

  所以无论对于认购还是认沽期权，vega增加，即波动率对期权价格的影响增加，期权的价格会上涨；vega降低，即波动率对期权价格的影响降低，期权的价格会下降。

  风险提示

  以上内容仅供参考

  以上就是股票里的gamma是什么？的详细内容，希望通过阅读小编的文章之后能够有所收获！