为什么叫勾股弦?
为什么叫勾股弦
接下来具体说说
“勾股弦”不只有特定值,任意“勾股弦”放线速度快不亚于经纬仪
看过几个用“勾股定理”给建筑物放直角线的视频,多是用“勾股定理”的特定值,比如勾3,股4,弦5。勾6,股8,弦10。还有勾1,股1,弦1.414等等。在这些视频的评论区的发言百花怒放,百家争鸣。
有人说这些特定值边长太小,先在墙角位置按这些数据量出直角,再延长两边误差太大,不能保证直角精度。还有人说还是用经纬仪放线更方便迅速,精度高等等。我想说经纬仪放线确实既快又方便,但是在没有经纬仪的情况下用任意大“勾股弦”放线也能保证高精度快速度。相信大家会认可我的理论和方法。
所谓任意“勾股弦”就是由任意两个建筑物的直角边按“勾股定理”的原理计算其对角线的长度,不局限于传统的3,4,5或者6,8,10。比如,一个长方形建筑物图纸上长边长为18米,短边为6米,那么由“勾股定理”可求得其对角线的长度为18.9737米。见图1

具体放线时,可按如下步骤操作:
1.首先在实地建筑物的长边位置用尺子量出18米,并在尺子的0和18的位置各钉一小钉1和2。见图2。

2.把尺子的0位置对准小钉1,拉紧尺子,分别以尺子的读数6和18.9737位置为半径在另两个角点的大概位置画圆弧a,b。见图3。
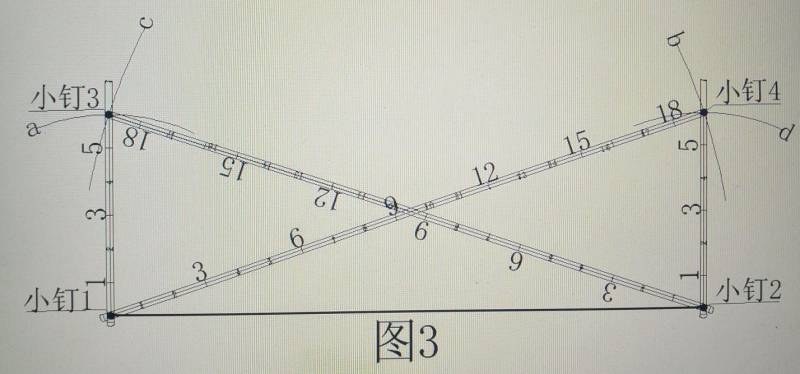
3 然后用同样方法把尺子的0位置对准铁钉2,拉紧尺子,分别以尺子读数18.9737和6的位置为半径在另两个角点的大概位置画圆弧c.,d。见图3。
4 a弧和c弧的交点即为角点3,钉小钉3。b弧和d弧的交点即为角点4,钉小钉4。见图3
5 在图3的小钉12431上依次拉上线绳即为该建筑物的外墙轮廓线。把四条直角边的连线延伸到龙门板或周围便于使用不被扰动的地方就可以管控此建筑物平面工程的施工,见图4。
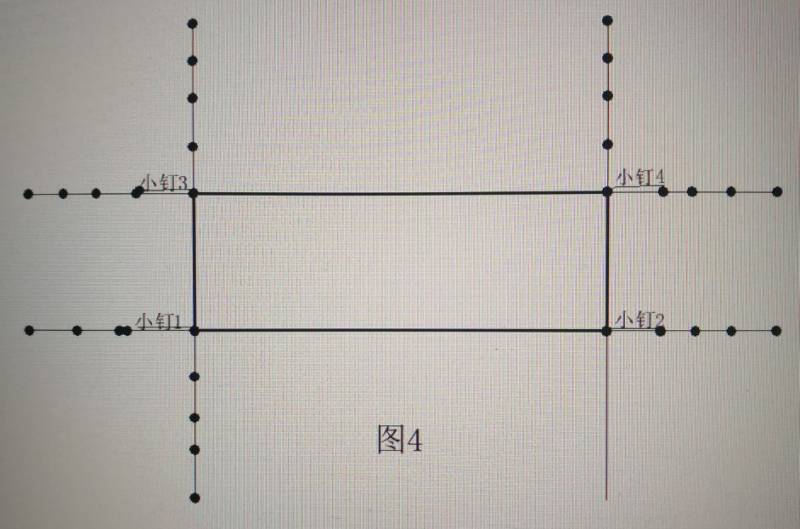
用这样的任意大”勾股弦”计算的大数据放样的长方形(或者正方形)只要操作精细,角点误差不会超过3毫米。
勾股定理的前世和今生
作为一个ex数学老师,好多人说,你一个理科生能不能干点正事?
咋的了,理科生就不能写历史了?理科也有理科的历史!
中国古代的理科生 刘徽、祖冲之、秦久韶、赵爽 等等,那都是可以跟华罗庚、苏步青之类的大师平起平坐的。
而且那时候,别说数学公式,连英文字母、阿拉伯数字也没有,遇到解方程问题,一大堆“ 天、地、人、物 ”来代表未知数,可知他们搞研究的难度有多大。

古代著作《九章算术》里让人看了就想打瞌睡的题目
为了让更多人知道我们理科生的前辈,我就试着讲讲“勾股定理”的一些事吧。
壹
首先得提一下《周髀》,这本书大约完成于公元1世纪,是中国最古老的天文学和数学著作,唐初还把它作为国子监明算科的教材,所以又叫《周髀算经》。
唐朝国子监数学教材《周髀算经》
关于这个国子监,那可真有点了不起。
课程安排里有选修课和必修课,每本教材都有教学计划、课时、学分。
必修课是儒家经书,有《春秋左传》《礼记》《诗经》等等,学习时间为一至三年不等。
选修课有书法、算数学、朝廷法令、书画鉴赏等,每门都有相应的学分。
同时,国子监还有考核制度,有季度考核、半期考核、整年考核、毕业考核。
这不就是现在的大学搞的那一套吗?选修、必修、考试、学分,原来那时候就已经有这种超前理念了。
国子监的教育理念如果能推广并延续下去,我想中国在科研方面的成绩要比现在牛得多了。
毕竟,能在国子监读书的可不是一般老百姓,受益面还是太小了。
在《周稗算经》首章里, 商高对周公说:
故折矩以为勾广三,股修四,径隅五。
这就是我们平时所说的“勾三股四弦五”的最早的出处。
商高还提到大禹那时候就已经掌握这一套知识了。
当然,上面所说边长分别为3、4、5的直角三角形只是一种特殊情况。
《周髀算经》中还明确记载了勾股定理的一般情况。
有一次荣方和陈子问答,陈子说:
若求邪至日者,以日下为勾,日高为股,勾股各自乘,并而开方除之,得邪至日。
就是说,要想算到太阳的距离,投影为勾,高度为股,将勾、股各平方后相加,再开方,就得到弦长。
这说明我国古代至迟在陈子所处年代,已经发现了勾股定理,并且还用他来测量至太阳的距离。
鹅说说”自制图凑合看看
遗憾的是,由于《周稗算经》记载的事情均为公元前11世纪至公元1世纪之间,那时候纸张还没有发明,所以传下来的资料有些残缺,只留下这些文字据后人猜测。
但是为纪念我们祖先的伟大成就,我国就将这个定理命名为勾股定理。
至于为什么用“勾、股”二字,我推测“股”是指大腿,“勾”含有弯曲的意思,大概指的就是膝关节以下的部位吧,这两者恰好可以组成两个直角边。
仅是猜测,不足为道。
贰
大约公元3世纪的 赵爽 ,他在研究《周稗算经》的时候,给批了注文,其中有一段又把勾股定理给描述了一下:
勾股各自乘,并之,为弦实,开方除之,即弦。
意思就是勾股数各自平方后相加,就是弦的平方,开方之后就是弦长。
简明扼要,干脆利落!
更重要的是,他给出了证明:
按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实。
看不懂吧,看不懂就对了,因为大家都看不懂。
赵爽给出的文字流传了下来,图形却失传了。
后人根据赵爽的文字推测了一下他的证明理论,并且复原了和文字配套的图形,我又根据后人的推测整理了一下证明步骤。
根据赵爽文字证明材料复原的几何图形
温馨提示: 下面这一大堆文字、字母可能会引起你的不适,请谨慎阅读。
证明: 不妨设勾=a,股=b,弦=c。显然,a,b,c也就是红色直角三角形的三边长。弦实和黄实为各自面积。 勾股相乘为朱实二: a乘以b等于一个红色三角形面积的2倍,即ab; 倍之为朱实四: 2ab等于一个红色三角形面积的4倍; 勾股之差自相乘为中黄实: (a-b) 2 等于中间黄*正方形面积的; 加差实,亦成弦实: 2ab+(a-b) 2 就是整个大正方形的面积。 这样一来,红色直角三角形的三条边a,b,c的关系就很明确了,即: a 2 +b 2 =c 2 。 证毕!
应该说,这个证明非常精彩, 2002年8月在北京召开的第二十四届国际数学家大会的会徽就是用的这个图。
第二十四届国际数学家大会明信片
但是,我们不能肯定,这就是赵爽最初的想法。
公元263年,魏晋时期的著名数学家 刘徽 在为古籍 《九章算术》 作注释时,也提出了一个勾股定理的证明,用的是“割补术”的方法:
勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂,开方除之,即弦也。
刘徽的证明原也有一幅图,可惜图也已失传。
但智慧的后人还是复原了他的证法图。
刘徽证明复原的几何图形(“钩”应为“勾”)
我怕引起大家第二次心理不适,这次就不详细讲解了,但还是很体贴地在网上找了个动图。
根据刘徽文字证明材料复原的动图
叁
这之后,中国古代数学家们对勾股定理的研究仍一直在继续,特别值得一提的就是清朝数学家 华蘅芳 。
华蘅芳从小也喜好数学,算得上是个学霸。
到20岁的时候,他已攻读了《周髀算经》《九章算术》《孙子算经》等上百多部我国古代知名算学著作,并且学习了明朝由传教士利玛窦引进我国的《几何原本》。
26岁的时候,他还写了本著作叫 《抛物线论》 ,给他配图的是科学家 徐寿 。
说起徐寿这个名字,你可能不知道,但提到元素周期表,你应该要知道一下。
元素周期表是俄国科学家门捷列夫发现的,是徐寿引进到中国来的。
而你现在见到的周期表里面那些 “镭、汞、钯、镧、钋、锂、钯” 等怪怪的字,正是徐寿从朱元璋后人的名字里找出来的。
因为老朱立下一条规矩,他后人的名字里必须要用“金、木、水、火、土”做偏旁,后来现存的字不够用了,就造了很多字。
他怎么也没想到,这条规矩竟然为元素周期表做出了这么大的贡献。
华蘅芳在研究数学问题的时候,顺便给勾股定理做出了二十多种证法。当然,和他在科学上的成就来比,勾股定理的证明只是冰山一角。
肆
可能有人知道,我说了这么久的“勾股定理”,在外国一般称为“毕达哥拉斯定理”。
毕达哥拉斯 是公元前六世纪古希腊数学家、哲学家,他自幼聪明好学,曾在名师门下学习几何学、自然科学和哲学。
毕达哥拉斯
后来他就到意大利的南部传授数学及宣传他的哲学思想,并和他的信徒们组成了一个所谓 “毕达哥拉斯学派” 。
这个学派的组织纪律很严密,甚至带有浓厚的宗教色彩,学员想要加入组织,除了要具备相当高的学术水平外,还要经历一系列神秘的仪式,并宣誓永不泄露学派的秘密和学说。
当时他的团队就研究出了直角三角形三边长的关系,但他们认为只有三边是整数时才符合这个定理,即勾股三元整数组。
打个比方,三角形三边长分别是5,12,13,因为5 2 +12 2 =13 2 ,可以说明这是直角三角形。
据说当时毕达哥拉斯取得了这一发现后非常兴奋,特地宰了一百头牛以示庆祝,所以勾股定理也叫 “百牛定理” 。
听上去真让人羡慕,那时候搞学术研究的经费挺充足的,一百头牛要值不少钱啊。
刚说了,毕达哥拉斯学派只认整数,如果把边长变成5/7,12/7,13/7,他们就不认可了。
因为在毕达哥拉斯学派眼里, 分数算不上严格意义上的数字。
放现在,我们用相似比的思想去理解一下就能想通了。
但可惜,他们并没有建立完整的相似理论。
毕达哥拉斯对这个定理的证明没有流传下来, 至于是因为他们的封闭没能公开,还是因为压根就没证明出来 ,这就不得而知了。
但是,由于西方认为这个思想是毕达哥拉斯学派首先提出来的,所以他们就把这个定理叫做毕达哥拉斯定理。
公元前4世纪,希腊数学家欧几里得在《几何原本》中给出一个证明,也是利用几何图形辅助证明。图在下面,自己去领悟吧。
欧几里得在《几何原本》中给出的证明动图
《几何原本》这本书相当牛,它是欧洲数学的基础,总结了平面几何五大公设,被广泛的认为是历史上最成功的教科书。
在西方,《几何原本》是仅次于《圣经》而流传最广的书籍。
流传度仅次于《圣经》的《几何原本》
伍
除了上面说的这些人,从古自今,尝试证明勾股定理的人非常之多。
《美国数学月刊》是数学家比较会关注的杂志,自1894年创办之日起,靠前期就开始刊登毕达哥拉斯定理的证明。
1901年,在连续刊登了第100个证明之后,杂志宣布: “该定理的证法是无穷无尽的,本刊今后将不再接受此类稿件”。
可有位《美国数学月刊》杂志的订阅户不干了,因为很多证明方法都是他收集或者自创后提供的。
我还没提供完毕呢,你们咋说不登就不登啊。
这位订阅户叫卢米斯,是一位中学教师。
1927年,已成为大学教授的他,一直没有停止对毕达哥拉斯定理的热爱,于是自己出版了 《毕达哥拉斯命题》 一书,收集了 230 个证法。
1940年,87岁的卢米斯又出版了该书的第二版,收集了 370 个证法。
最后,用一个真实的事情结尾。其实这件事上一篇提过了,有人还以为是我编的一个段子。
1977年,中国科学院院士 潘承彪 教授受国家教育部委托,为靠前届恢复高考的数学卷子出个解答题。
潘承彪与亲哥哥潘承洞
潘教授考虑到这次考试的重要意义,本着“鼓励学生、送分上门”的原则,出了一道他认为相当简单的题: 请证明勾股定理。
这题对他来说,自然是非常简单,因为那时候他正在和哥哥潘承洞一起研究世界难题“哥德巴赫猜想”。
至于对学生来说的话,就有点那什么了。
据说考场里的学生见到这道题的时候,开始还挺高兴,可一会儿就变脸了,再然后,就有人开始哭了。
道理我都懂,可就是不知道该怎么写。
试卷批出来了,最后统计,这道题的正确率不足1%。
听说后来有人议论这道题的时候,潘教授都是躲着走。
见到知情的同事,一个劲儿地嘱咐: 人家要问,你可千万别说那道题是我出的啊。
以上就是为什么叫勾股弦?的详细内容,希望通过阅读小编的文章之后能够有所收获!
