00010000的十进制是多少?
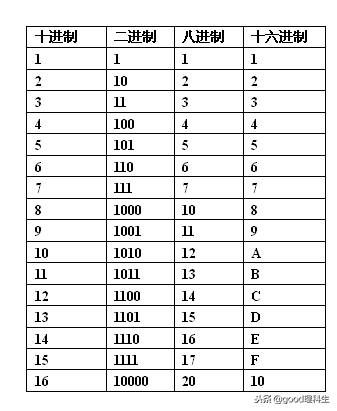
00010000的十进制是多少
进制转化为十进制怎么算?二进制是计算机中最基本的数制。在二进制中,每位上只有两个数值:0和1。相比之下,十进制则是我们日常生活中最常使用的数制,其中每位上有0到9的十个数值。接下来具体说说
二进制数转换为十进制数、八进制数、十六进制数的方法
与十进制

(1)二进制转十进制
方法:“按权展开求和”
【例】:
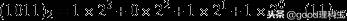
规律:个位上的数字的次数是0,十位上的数字的次数是1,......,依次递增,而十
分位的数字的次数是-1,百分位上数字的次数是-2,......,依次递减。
注意:不是任何一个十进制小数都能转换成有限位的二进制数。
(2)十进制转二进制
· 十进制整数转二进制数:“除以2取余,逆序排列”(除二取余法)
【例】:
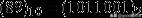
89÷2 ……1,44÷2 ……0,22÷2 ……0,11÷2 ……1,5÷2 ……1,2÷2 ……0,1
十进制小数转二进制数:“乘以2取整,顺序排列”(乘2取整法)
【例】: (0.625)10= (0.101)2
0.625X2=1.25 ……1
0.25 X2=0.50 ……0
0.50 X2=1.00 ……1
十进制1至128的二进制表示:
0=0
1=1
2=10
3=11
4=100
5=101
6=110
7=111
8=1000
9=1001
10=1010
11=1011
12=1100
13=1101
14=1110
15=1111
16=10000
17=10001
18=10010
19=10011
20=10100
21=10101
22=10110
23=10111
24=11000
25=11001
26=11010
27=11011
28=11100
29=11101
30=11110
31=11111
32=100000
33=100001
34=100010
35=100011
36=100100
37=100101
38=100110
39=100111
40=101000
41=101001
42=101010
43=101011
44=101100
45=101101
46=101110
47=101111
48=110000
49=110001
50=110010
51=110011
52=110100
53=110101
54=110110
55=110111
56=111000
57=111001
58=111010
59=111011
60=111100
61=111101
62=111110
63=111111
64=1000000
65=1000001
66=1000010
67=1000011
68=1000100
69=1000101
70=1000110
71=1000111
72=1001000
73=1001001
74=1001010
75=1001011
76=1001100
77=1001101
78=1001110
79=1001111
80=1010000
81=1010001
82=1010010
83=1010011
84=1010100
85=1010101
86=1010110
87=1010111
88=1011000
89=1011001
90=1011010
91=1011011
92=1011100
93=1011101
94=1011110
95=1011111
96=1100000
97=1100001
98=1100010
99=1100011
100=1100100
101=1100101
102=1100110
103=1100111
104=1101000
105=1101001
106=1101010
107=1101011
108=1101100
109=1101101
110=1101110
111=1101111
112=1110000
113=1110001
114=1110010
115=1110011
116=1110100
117=1110101
118=1110110
119=1110111
120=1111000
121=1111001
122=1111010
123=1111011
124=1111100
125=1111101
126=1111110
127=1111111
128=10000000
十进制负数转二进制:“先取正数的二进制值,再取反,加1”
【例】:(-31)10 = (1)2
31的二进制数为11111,取反00000,加1得1。
与八进制
二进制数转换成八进制数:从小数点开始,整数部分向左、小数部分向右,每3位为一组用一位八进制数的数字表示,不足3位的要用“0”补足3位,就得到一个八进制数。
八进制数转换成二进制数:把每一个八进制数转换成3位的二进制数,就得到一个二进制数。
八进制数字与十进制数字对应关系如下:
000 -> 0 | 004-> 4 | 010=8
001 -> 1 |005 -> 5| 011=9
002 -> 2 |006 -> 6 | 012=10
003 -> 3 |007 -> 7 | 013=11
【例】:将八进制的37.416转换成二进制数:
3 7 . 4 1 6
011 111 .100 001 110
即:(37.416)8 =(11111.10000111)2
【例】:将二进制的10110.0011 转换成八进制:
0 1 0 1 1 0 . 0 0 1 1 0 0
2 6 . 1 4
即:(10110.0011)2 = (26.14)8
与十六进制
二进制数转换成十六进制数:二进制数转换成十六进制数时,只要从小数点位置开始,向左或向右每四位二进制划分一组(不足四位数可补0),然后写出每一组二进制数所对应的十六进制数码即可。
十六进制数转换成二进制数:把每一个十六进制数转换成4位的二进制数,就得到一个二进制数。
十六进制数字与二进制数字的对应关系如下:
0000 -> 0 0100 -> 4 1000 -> 8 1100 -> C
0001 -> 1 0101 -> 5 1001 -> 9 1101 -> D
0010 -> 2 0110 -> 6 1010 -> A 1110 -> E
0011 -> 3 0111 -> 7 1011 -> B 1111 -> F
【例】:将十六进制数5DF.9 转换成二进制:
5 D F . 9
0101 1101 1111 .1001
即:(5DF.9)16 =(10111011111.1001)2{十六进制怎么会有小数点}
【例】:将二进制数1100001.111 转换成十六进制:
0110 0001 . 1110
6 1 . E
即:(1100001.111)2 =(61.E)16
与十进制的区别
二进制与十进制的区别在于数码的个数和进位规律有很大的区别,顾名思义,二进制的计数规律为逢二进一,是以2为基数的计数体制。10这个数在二进制和十进制中所表示的意义完全不同,在十进制中就是我们通常所说的十,在二进制中,其中的一个意义可能是表示一个大小等价于十进制数2的数值。
仿照例题1.3.1,我们可以将二进制数10表示为:10=1×2^1+0×2^0
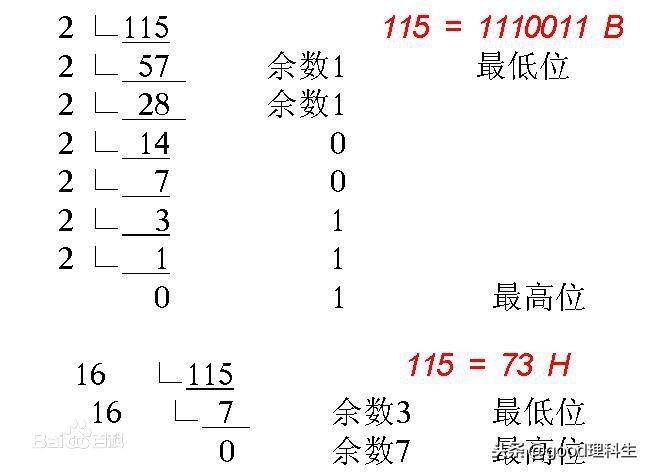
十进制与二进制的关系
一般地,任意二进制数可表示为:
例题 1.3.2 试将二进制数(01010110)B转换为十进制数。
解:将每一位二进制数乘以位权后相加便得相应的十进制数
在数字电子技术和计算机应用中,二值数据常用数字波形来表示。使用数字波形可以使得数据比较直观,也便于使用电子示波器进行监视。
用二进制数的数字编码波形图
二进制、八进制、十进制和十六进制数制转换
一、数制
1、什么是数制
数制是计数进位的简称。
也就是由低位向高位进位计数的方法。
2、常用数制
计算机中常用的数制有二进制、八进制、十进制和十六进制。
3、数制的特点
二进制:基数为2,数值部分用2个不同的数字符号0、1来表示;进位规则是逢二进一。
八进制:基数是8,有8个数字符号:0、1、2、3、4、5、6、7;进位规则是逢八进一。
十进制:基数是10,有10个数字符号:0、1、2、3、4、5、6、7、8、9;进位规则是逢十进一。
十六进制:基数是16,它有16个数字符号,除了十进制中的10个数可用外,还使用了6个英文字母:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A-F分别代表十进制数的10-15;进位规则是逢十六进一。
4、数制的表示方法
二进制数:1101B或(1101) 2
八进制数:0125或125Q或(125) 8
十进制数:368D、368或(368) 10
十六进制数:4A31H、0x4A31或(4A31) 16
二、数制转换
1、二进制、八进制、十六进制转换为十进制
方法:按权展开求和
按权展开
2、十进制转换为二进制、八进制、十六进制
整数部分与小数部分需要分别转换.
(1)十进制整数转换为二进制整数
方法:除二取余,倒序排列
将要转换的十进制整数除以2取余;再用商除以2,再取余法,直到商等于0为止,将每次得到的余数按倒序的方法排列起来即为结果。
例:37 =(100101) 2
(2)十进制整数转换八进制、十六进制整数
方法:除八取余,倒序排列;
例:237= ( 355 ) 8
方法:除十六取余,倒序排列
例:169= ( A9 ) 16
(3)十进制小数转换成二进制小数
方法:乘二取整,正序排列
将要转换的十进制小数乘以2取整数;再用小数乘以2,再取整数,直到积的小数部分为0或保持所需精度为止,将每次得到的整数按正序的方法排列起来即为结果。
例:0.375 =( 0.011 ) 2
(4)十进制小数转换八进制、十六进制小数
方法:乘八取整,正序排列;
例:0.3125 = ( 0.24 ) 8
方法:乘十六取整,正序排列;
例:0.5 = ( 0.8 ) 16
3、二进制、八进制、十六进制之间互相转换
(1)二进制转八进制
方法:将二进制数由小数点开始,整数部分向左,小数部分向右,每3位一组,不够3位补0,把每组二进制数按权展开相加转换为1个八进制数。
例:( 1101010.01 ) 2 = ( 152.2 ) 8
(2)八进制转二进制
方法:将每位八进制数转为3位二进制数,不够3位补0。
例:( 67 ) 8 =( 110111 ) 2
(3)二进制转十六进制
方法:从小数点开始向左向右把二进制每4个分成一组,不够4位补0,然后把每一组二进制数按权展开相加转换为1个十六进制数。
例:( 100111100 ) 2 = ( 13C ) 16
(4)十六进制转二进制
方法:将每位十六进制数转为4位二进制数,不够4位补0。
例:( A5F8 ) 16 = ( 1010010111111000 ) 2
(5)八进制转十六进制
方法:将八进制数先转换为二进制数,再4位一组转换为为十六进制数。
例:( 254 ) 8 = ( AC ) 16
(6)十六进制转八进制
方法:将十六进制数先转换为二进制数,再3位一组转换为八进制数。
例:( 5F8 ) 16 = ( 2770 ) 8
二进制**为十进制怎么算?这种简单计算方法看一看
二进制**为十进制怎么算?二进制是计算机中最基本的数制。在二进制中,每位上只有两个数值:0和1。相比之下,十进制则是我们日常生活中最常使用的数制,其中每位上有0到9的十个数值。下面就给大家介绍一下进制转换的操作步骤。
当我们需要将二进制**为十进制时,我们需要按照以下步骤执行:
- 从右至左,对每一位上的数值进行编号,从0开始。
- 对于每个二进制位,将它对应的数字乘以2的编号次方。
- 将上一步得到的乘积相加,得到最终的十进制数值。
例如,假设我们有一个8位二进制数:11001101。我们可以按照上述步骤将它**为十进制数值:
- 从右至左,对每一位上的数值进行编号,从0开始。这个数的最右边一位是第0位,最左边一位是第7位。
- 对于第0位,它对应的数字是1,因此我们将1乘以2的0次方,得到1。
- 对于第1位,它对应的数字是0,因此我们将0乘以2的1次方,得到0。
- 对于第2位,它对应的数字是1,因此我们将1乘以2的2次方,得到4。
- 对于第3位,它对应的数字是1,因此我们将1乘以2的3次方,得到8。
- 对于第4位,它对应的数字是0,因此我们将0乘以2的4次方,得到0。
- 对于第5位,它对应的数字是0,因此我们将0乘以2的5次方,得到0。
- 对于第6位,它对应的数字是1,因此我们将1乘以2的6次方,得到64。
- 对于第7位,它对应的数字是1,因此我们将1乘以2的7次方,得到128。
- 将上述结果相加,得到1+0+4+8+0+0+64+128=205。
因此,11001101的十进制数值为205。
随着现在科技的发展,现在已经有可很多数学计算工具可以帮助我们进行进制转换的计算了,例如Mathtool就是一款很好用的计算工具。只需要进入网站当中,点击【二进制转十进制】
接着,输入需要转换的二进制数,最后点击【计算】就可以了。
以上就是00010000的十进制是多少?的详细内容,希望通过阅读小编的文章之后能够有所收获!
